Ce que je retiens des tableaux et calculs vectoriels avec NumPy (1/2)

Le plus simple pour créer un tableau est la fonction array

arr = np.array(data)

où data est par exemple une liste que je peux initialiser avec des 0.

data = [0] * 5

Euh nan disons plutôt avec des valeurs différentes.

data = [0 for i in range(5)]

J’aurais peut-être du préciser le type de mes données

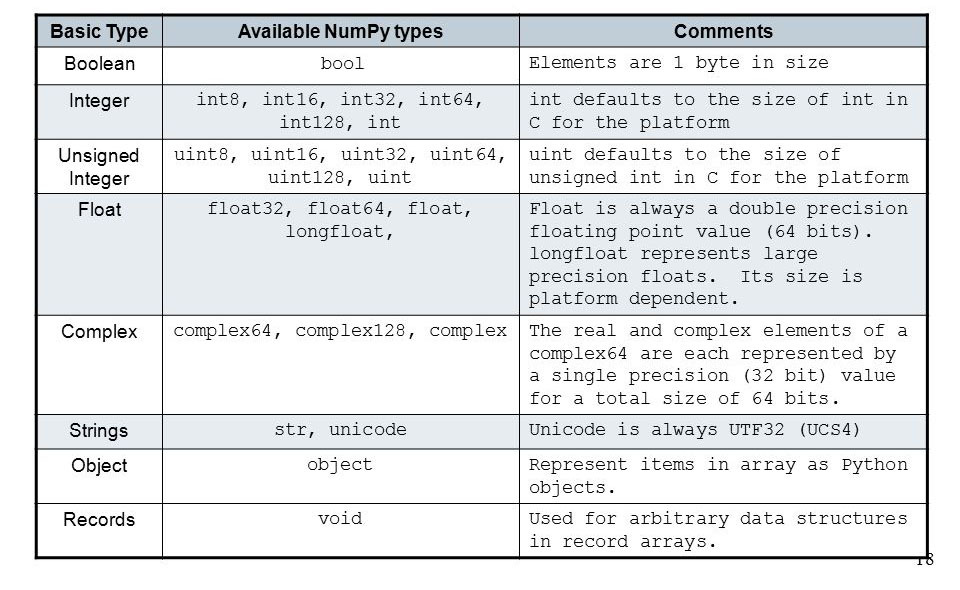
arr = np.array(data, dtype=np.int32)

J’imagine que l’intérêt principal est d’économiser de la place en mémoire (?).Le moins que l’on puisse dire c’est qu’il y en a un paquet.

Source : https://www.simplifiedpython.net/python-numpy/

Et voilà on a un beau array de dimension

data.shape

C’est nul, pas assez de dimensions

data2 = [[0, 8], [0, 7]]

C’est mieux. Mais plutôt que d’initialiser à la main, j’aurais pu

np.zeros(10)

ou

np.ones((5,6))

Tous les éléments doivent être du même type quand même

Je peux le vérifier avec

data.dtype

Sinon il faudra caster

arr_ = arr.astype(np.float64)

Bien sûr une chaîne de caractères ne peut pas être convertie en float.

Entrons dans le vif du sujet : les opérations

Ces tableaux permettent donc de faire des opérations sans avoir à parcourir les éléments.

Si les tableaux sont de mêmes dimensions :

data+data

Et les opérations avec des scalaires propagent la valeur sur chaque élément.

data*10

Si les tailles différents, ils appellent ça le broadcasting.

Ensuite pour ce qui est de l’indexation

Quand je broadcast une valeur à une tranche comme ceci

arr[0:8] = 12

L’array d’origine est modifié directement. La tranche n’est pas une copie temporaire (pour des questions de performance).

Pour faire une copie, il existe

arr[0:8].copy()

Pour les tableaux à plusieurs dimensions, les éléments sont accesibles via les indices

arr[0, 8]

ou

arr[0][8]

Pour faire professionnel, le plus intéressant est encore d’utiliser les deux points quand c’est possible

arr[0:8]

Cela signifie prendre l’axe en entier

Source : Analyse de données en Python (livre)

On peut aussi chercher une étiquette. Je dis étiquette mais c’est plutôt chaîne de caractères.

arr[names == 'Bob']

Où l’array serait

arr = np.array([‘Bob’, ‘Toto‘])

J’ai découvert qu’on pouvait carrément rechercher tout sauf Bob

arr != 'Bob'

ou

arr[-(names == 'Bob')]

Je me demande si des personnes utilisent cette syntaxe.

Maintenant transposons

La transposition c’est une forme particulière de redimensionnement. En fait,

arr = np.arange(15).reshape((3, 5))

arr
#res

arr.T
#res

fezf

et ils utilisent souvent (apparemment) la méthode dot

np.dot(arr.T, arr)

pour les tableaux de dimensions supérieures, transpose accepte un tuple de numéros d’axes pour permuter les axes.

arr.transpose((1, 0, 2))

Passons en revue les universal function

np.sqrt(arr)
np.exp(arr)

x = np.random.randn(8)
y = np.random.randn(9)
np.maximum(x, y)

Bon, on ne va pas toutes les faire.

Plus intéressant : les conditions sur les tableaux

En fait, on peut produire un tableau à partir d’un tableau existant avec des conditions.

res = np.where(arr > 2, 1, 0)

c’est-à-dire pour toutes les valeurs > 2 dans le tableau, on remplace par 1.

Et pour faire l’équivalent de

if cond1[i] and cond2[i]:
    resul.append(0)
elif cond1[i]:
    result.append(1)
elif cond2[i]:
    result.append(2)
else:
    result.append(3)

On fait :

np.where(cond1 & cond2, 0, 
         np.where(cond1,1, 
                  np.where(cond2, 2, 3)))

C’est démentiel !

Pour ce qui est des statistiques

J’ai noté :

• sum pour faire la somme

• mean la moyenne

• std la déviation et var la variance

• min et max pas besoin de le dire

• argmin et argmax les indices des éléments min et max

• cumsum pour la somme cumulée des éléments à partir de 0

• cumprod la même chose mais à partie de 1

Avant de faire ces calculs, j’aurais peut-être du trier mon tableau

arr.sort()

Ou récupérer les valeurs uniques

np.unique(arr)

Enfin en terme d’algèbre linéaire

Pour la multiplication matricielle

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
np.dot(x, y)

ou

x.dot(y)

J’ignore la différence.

Il y en a pas mal : diag, trace, det, eig, inv, pinv, qr, svd, solve, lstsq…